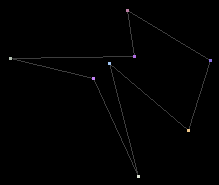
Dado un conjunto de puntos sobre el plano, llamo constelación a un recorrido cerrado que una todos los puntos y que no se corte a sí mismo.
El problema es simple: demostrar que todo conjunto de N puntos (N > 2) tiene una constelación, o encontrar algún contraejemplo.
(Update: pueden probar el jueguito que estaba haciendo cuando se me ocurrió la pregunta. El juego usa otro tipo de constelación.)
5 comentarios:
si no entendí mal, un contraejemplo serían N puntos colocados en línea recta.
Saludos
Interesante el problema.
Me parece que si suponemos que existe al menos un punto que no sea colineal con el resto, la demostración es sencilla:
Se escoge un punto arbitrario del plano como referencia, que por comodidad conviene que este "centrado" entre los puntos. Hacemos un barrido en ángulo a partir de este punto y vamos agregando los puntos al recorrido en el orden que van siendo detectados (los empates se visitan alejándose del centro).
Para hacerlo más claro: el barrido es como si hubiese un segundero girando en el punto de referencia, y que a medida que avanza, cada vez que aparece un nuevo punto lo agregamos al recorrido.
Este método siempre forma una constelación. No se me ocurre una demostración sencilla para esto, pero debe haberla. Probablemente ayudaría imaginar los segmentos con dirección, porque todos tienen la misma orientación respecto al punto central.
Se me ocurren otras demostraciones que sí son completas pero un poco menos elegantes:
- Se puede mostrar que por medio de una permutación de arcos siempre se puede eliminar un cruce en particular, entonces podemos tomar cualquier ciclo como punto de partida, y eliminar sucesivamente sus cruces hasta obtener una constelación.
- Se puede mostrar que siempre se pueden unir dos constelaciones para formar una nueva (una forma sería agregar uno de los arcos de la envolvente de los puntos), entonces podemos partir de triángulos y cuadriláteros aislados y unirlos sucesivamente para obtener una constelación.
- También podríamos mostrar que siempre se puede agregar un nuevo punto a una constelación, y después aplicar inducción.
Saludos!
¡Gracias ambos por los comentarios!
Me doy cuenta de que tendría que haber agregado la restricción de que ningún trío de puntos es colineal.
Además ahora me doy cuenta de que siempre se puede descruzar un recorrido que se cruce...
Pensaré alguna otra variante menos sencilla.
Yo conocía una variante de este problema con n elementos rojos y n elementos azules tales que ningún trío estaba alineado y que debían aparejarse sin que los segmentos que unían un rojo y un azul se cruzaran.
De ese problema se extrae una idea interesante respecto a descruzar parejas de arcos: jamás se puede ciclar haciendo ese procedimiento.
Esto es importante porque quizá para algún conjunto de 2n puntos es posible que cada vez que descruzamos una pareja de arcos se cruce la siguiente y el círculo se complete volviendo al estado inicial.
Pero bien, esto no puede pasar porque los arcos descruzados siempre tienen una longitud (conjunta) menor que los arcos cruzados de manera que cada vez que descruzamos dos arcos estamos reduciendo la longitud total de los arcos de toda la constelación.
Por lo tanto basta con unir los puntos de manera cíclica en cualquier orden y luego ir descruzando arcos hasta obtener una constelación. Se trata de un proceso finito y bien definido.
Ahora bien, se me ocurre una pregunta al respecto: ¿La configuración final es siempre la misma o depende de la configuración inicial y/o el orden en el que se descruzan las ramas?
¡Gracias Carlos!
Muy buena la pregunta final...
Publicar un comentario