Los dos arcos

Sobre una esfera elegimos cuatro puntos al azar, y los unimos de a dos con arcos mínimos.
¿Cuál es la probabilidad de que los dos arcos compartan algún punto, como en la imagen?

El segmento monocromático

Demostrar o refutar lo siguiente:

De cualquier forma que pintemos el plano con dos colores, siempre habrá un segmento unitario cuyos puntos sean todos de un mismo color.

Burr Tools, una gran herramienta

Recomiendo este programa a todos los que gusten de inventar problemas de empaquetamiento o cardos.

Empaquetando círculos

Tenemos N círculos, cuyos radios van de 1 a N.
¿Cómo empaquetarlos de manera que quepan (sin solaparse) en el círculo más chico posible?

Update: Al parecer este problema se usó en este concurso hace tiempo.

Plano y colores

Alguien pintó el plano de 3 colores.

¿Se puede asegurar que habrá siempre 3 puntos equidistantes entre sí y que sean o bien todos del mismo color o bien todos de diferente color?

Hipercaja

¿Se puede llenar una hipercaja de 5x6x7x8 con hiperladrillos de 1x2x3x4?

(parafraseado de un problema de la olimpíada Paenza que me comentó Julián)

Constelaciones

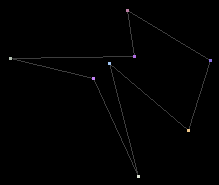
Dado un conjunto de puntos sobre el plano, llamo constelación a un recorrido cerrado que una todos los puntos y que no se corte a sí mismo.

El problema es simple: demostrar que todo conjunto de N puntos (N > 2) tiene una constelación, o encontrar algún contraejemplo.

(Update: pueden probar el jueguito que estaba haciendo cuando se me ocurrió la pregunta. El juego usa otro tipo de constelación.)

Triángulos

Este problema es una idea derivada de uno que vi aquí. Allí demuestran que ningún triángulo puede tener lados distintos e iguales a tres números de Fibonacci.

Me pregunto: ¿habrá un conjunto más denso que el de Fibonacci que cumpla lo mismo?

Con denso me refiero a haya menos espacio entre términos sucesivos (se puede definir de muchas maneras, pero supongo que entenderán el sentido intuitivo).

Concurso de empaquetamiento de puntos

¿Cuán pequeño puede ser el mínimo círculo que circunde a N puntos, si los puntos tienen que tener coordenadas enteras y no repetir distancias entre ellos?

Tal es el tema del concurso de Al Zimmermann de esta temporada. En este sitio se puede leer las reglas, anotarse y comenzar a enviar soluciones.

Árboles cuadriculados

El otro día me puse a dibujar árboles siguiendo las líneas de una hoja cuadriculada, como en la figura. (Básicamente, un árbol es un grafo conexo sin ciclos).

¿Cuántos árboles de N nodos se podrán dibujar? (Todas las intersecciones del cuadriculado usadas cuentan como nodos).

La taza inclinada

Este es un problema sacado del mundo real.

Mi amigo Javier tiene una cafetera, y tazas con forma de cono truncado. En la figura se ve la taza de perfil. Tanto la base como el fondo son círculos.

Cuando mi amigo quiere meter o sacar la taza de la cafetera, debe inclinarla un cierto ángulo. ¿Cuánto café puede servir, como máximo, para que al retirar la taza no se vuelque café? La parte sombreada de la figura representa el café cuando la taza está inclinada.

Las hormigas

Tres hormigas puntuales caminan por un campo cuadrado, con velocidad constante y rebotando perfectamente en sus bordes.

Para cada valor natural de K, queremos encontrar puntos iniciales, velocidades y direcciones para las hormigas, tales que haya exactamente K puntos distintos del cuadrado en los que las hormigas coincidan, caminando lo suficiente.

¿Se podrá hacer para todo K?

Una vez logrado para cierto K, ¿coincidirán las hormigas una cantidad finita o infinita de veces en esos puntos?

Uniendo triángulos

Tenemos 13 triángulos equiláteros iguales entre sí. Fijamos uno de ellos al plano, y vamos fijando los demás uno por uno, de manera que uno y sólo uno de sus lados coincida exactamente con un lado de un triángulo ya fijado.


¿Cuántas figuras distintas podremos armar?